Clase del viernes, 5 de abril del 2019
En esta clase, pudimos aprender acerca de los números complejos y su forma polar y rectangular
NÚMEROS COMPLEJOS
Los números complejos conforman un grupo de cifras resultantes de la suma entre un número real y uno de tipo imaginario.
los números complejos se emplean en diversos campos de las matemáticas, en la física y en la ingeniería. Por su capacidad para representar la corriente eléctrica y las ondas electromagnéticas, por citar un caso, son utilizados con frecuencia en la electrónica y las telecomunicaciones. Y es que el llamado análisis complejo, o sea la teoría de las funciones de este tipo, se considera una de las facetas más ricas de las matemáticas.
Representación geométrica de un número complejo.Sea z = a + b·i un número complejo en forma binómica. Su expresión en forma cartesiana es
z = (a,b). Consideremos el plano euclídeo real R2, y en él un sistema de referencia ortonormal. A cada número complejo z = a + b·i le hacemos corresponder un punto del plano P(a,b); y recíprocamente, dado ese punto del plano le asociamos el complejo z = a + b·i. Tenemos pues una biyección entre el plano euclídeo real R2 y el cuerpo de los núneros complejos C.
El punto del plano P(a,b) correspondiente al complejo z = a + b·i recibe el nombre de afijo de z. El ángulo que forma el vector OP con el eje de abcisas recibe el nombre de argumento de z.
Además, el módulo del vector OP es:
|OP| = (a2 + b2)1/2 = |z|
que coincide con la distancia del punto P al origen de coordenadas.
Sea r = |z|. Si x es su argumento, se tiene que:
sen x = PA/OP = b/r ==> b = r·sen x
cos x = OA/OP = a/r ==> a = r·cos x
Luego podernos escribir z = a + b·i = r·cos x + i·r·sen x = r·(cos x + i·sen x)
Forma trigonométrica y forma polar.
Esta expresión, z = r·(cos x + i·sen x), recibe el nombre de forma trigonométrica de z, donde r es el módulo de z y x su argumento. Definimos la forma polar del número complejo z = r·(cos x + i·sen x) como rx.
Igualdad de números complejos en forma trigonométrica.
Veamos cuando dos complejos en forma trigonométrica, o en forma polar, son iguales:
Sean z1 = r·(cos x + i·sen x) y z2 = r´·(cos y + i·sen y). Si z1 = z2, entonces r·(cos x + i·sen x) = r´·(cos y + i·sen y). Como dos números complejos iguales tienen el mismo módulo, entonces r = r´, y por tanto, (cos x + i·sen x) = (cos y + i·sen y), de donde:
cos x = cos y ==> y = x + 2·k·pi, con k C Z
sen x = sen y
Por tanto, r·(cos x + i·sen x) = r·[cos (x + 2·k·pi) + i·sen(x + 2·k·pi)], y en forma polar resulta:
rx = rx + 2·k·pi
Paso de la forma binómica a la forma polar
Hemos visto que z = a + b·i = r·(cos x + i·sen x) = r·cos x + i·r·senx, de donde:
a = r·cos x
b = r·sen x
Por otra parte, sea z = a + b·i un número complejo en forma binómica. Por definición tenemos que:
|z| = (a2 + b2)1/2
Además es:
b/a = (r·sen x)/(r·cos x) = (sen x)/(cos x) = tg x
Por tanto
x = arc tg (b/a)
estudiando el cuadrante de x según los signos de la parte real y de la parte imaginaria le z.

Videos donde podremos entender mejor...
Transformación de rectangular a polar
Transformación de polar a rectangular
Ahora emplearemos los siguientes conceptos en el tema de Corriente Alterna...
CORRIENTE ALTERNA
La corriente alterna es aquel tipo de corriente eléctrica que se caracteriza porque la magnitud y la dirección presentan una variación de tipo cíclico. En tanto, la manera en la cual este tipo de corriente oscilará es en forma senoidal, es decir, una curva que va subiendo y bajando continuamente. Gracias a esta forma de oscilación la corriente alterna logra transmitir la energía de manera más eficiente.
La forma de oscilación de la corriente alterna más comúnmente utilizada es la oscilación senoidal1con la que se consigue una transmisión más eficiente de la energía, a tal punto que al hablar de corriente alterna se sobrentiende que se refiere a la corriente alterna senoidal.

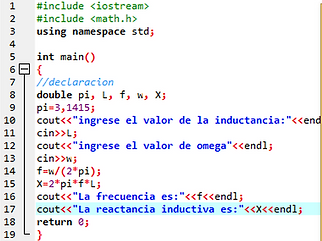
Para comenzar mostraré como podemos aplicar los números complejos en C++
En este documento podremos encontrar como elaborar nuestro C++, para la transformación de polar a rectangular o viceversa
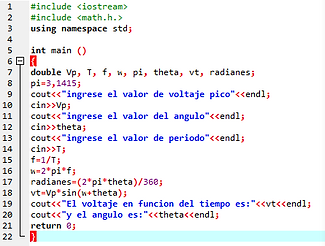
Ahora les mostraré algunas formulas de la corriente alterna en C++
Como hallar el voltaje con respecto al tiempo
Como hallar la REACTANCIA INDUCTIVA